Avsnitt 7 Flerfaktorsanalys

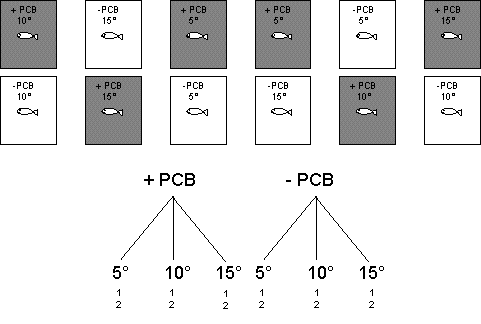
Detta kapitel behandlar hur man analyserar och tolkar experiment som innehåller mer än en experimentell faktor. Sådana experiment kallas ibland för multifaktoriella. I föregående kapitel diskuterades experiment med en eller flera nestade faktorer. Dessa utmärktes av att nivåerna i en faktor var unika för varje nivå av den andra faktorn. En annan typ av experimentell faktor, som kallas ortogonal, innebär att varje nivå av en faktor finns inom varje nivå av den andra faktorn. Som ett exempel kan vi betrakta ett experiment där vi är intresserade att undersöka effekten av PCB på tillväxten hos fiskar i olika temperaturer (se figur nedan där varje fisk gärna kan ha ett unikt nummer eftersom det är olika individer i de olika akvarierna).

I experimentet placerar vi en fisk i varje akvarium. För varje kombination av temperatur och PCB-koncentration har vi två akvarier. För alla tre temperaturer har vi två akvarier med PCB och två utan. Omvänt har vi för båda koncentrationerna två akvarier för varje temperatur. Man säger att koncentrationen av PCB är ortogonal mot temperaturen. Notera skillnaden mot exemplet med nestade akvarier i förra avsnittet.

I kursbokens tabell 10.1 illustreras på liknande sätt skillnaden mellan ortogonala och nestade experimentuppställningar. Båda typer är lämpliga för ekologiska experiment, men i olika sammanhang (man bör däremot undvika mellanting som i tabell 10.1c!). Experiment med ortogonala faktorer behövs för att man skall kunna undersöka om effekten av en faktor är oberoende av en annan faktor. Om, till exempel, effekten av PCB på tillväxten hos fiskar ökar med ökande vattentemperatur så är det inte meningsfullt att uttala sig generellt om betydelensen av PCB för tillväxten av fiskar, utan att ta hänsyn till temperaturförhållandena där fisken lever. Detta kallas för att faktorerna interagerar (=samspelar). Det kanske viktigaste målet med detta kapitel är att du på ett konkret sätt skall kunna förstå innebörden av en sådan interaktion! Detta diskuteras på ett lättfattligt sätt i styckena 10.3, 10.5 och 10.6.

Stycke 10.2 och 10.4 går i detalj in på hur man beräknar summan av de kvadrerade avvikelserna (SS) och frihetsgrader (df) för interaktioner och enskilda faktorer (ibland kallade huvudfaktorer eller "main effects"). Som en tumregel kan man säga att huvudfaktorernas frihetsgrader beräknas på samma sätt som i enfaktors ANOVA och att interaktionens frihetsgrader fås genom att man multiplicerar frihetsgraderna för de faktorer som ingår i interaktionen. Figurerna 10.1 och 10.2 är viktiga! Studera dem noga! Jämför dem med figurerna 9.2 och 9.3 och med formlerna 9.2 och 10.7. Att i detalj förstå hur SS beräknas för interaktioner är relativt komplicerat och inte helt nödvändigt för att du skall kunna förstå vad interaktionen innebär och hur man utför analyserna i praktiken.

När man planerar faktoriella experiment är det extra viktigt att man klargör vilka faktorer som är fixerade och slumpade. Detta beror ytterst på att hypoteserna för slumpade och fixerade faktorer är olika. Det är viktigt här att känna till att (1) nämnaren i F-kvoterna skiljer sig mellan slumpade eller fixerade faktorer och att (2) detta beror på att de ingående varainskomponenterna i MS-skattningen för huvudfaktorerna skiljer sig åt. I tabell 10.8 beskrivs alla tänkbara kombinationer för experiment med två ortogonala faktorer. Den högra kolumnen visar vilka termer som skall användas för att bilda F-kvoter för huvudfaktorer ochh interaktioner. Var säker på att du med hjälp av den föregående kolumnen ("Mean square estimates") förstår varför en viss MS används som nämnare i de olika F-kvoterna. F-kvoten bildas så att nämnaren innehåller alla varianskomponenter som finns i täljaren, förutom den komponent som beror på faktorn som man vill testa. Till exempel i tabell 10.8b testas den fixerade faktorn A över interaktionen A x B eftersom MSA innehåller samma komponenter som MSAxB plus komponenten som beror av faktorn A. Om MSA är signifikant större än MSAxB vet vi att detta beror på att bidraget från A (k²_A) är större än 0. Om du på detta plan förstår hur F-kvoterna bildas kan du förstå och utföra alla typer av test med mer komplicerade experimentuppställningar, även om du inte till fullo förstår hur SS beräknas algebraiskt.

En annan användbar kunskap från kapitlet är hur man går vidare med multipla jämförelser i experiment med flera faktorer (stycke 10.8). Notera att om en interaktion visar sig vara signifikant går man ej vidare och testar enskilda huvudfaktorer. Istället genomför man multipla jämförelser på interaktionen. Detta gäller framförallt fixerade faktorer.

Resten av kapitel 10 behandlar utveckling av faktoriella experiment till tre faktorer, statistisk styrka m.m.. Detta är ämnen som är högst relevanta inom ekologisk forskning men för denna kurs betraktar vi det som överkurs.

Lösta exempel

Procedur för 2-faktors ANOVA i Excel.

Genomarbetade exempel från kursboken.  

Dessa kapitel kommer inte att behandlas närmare under kursen. För dig som skall planera komplicerade flerfaktoriella experiment kan dock dessa kapitel utgöra en värdefull "kokbok" och uppslagsbok när det gäller att utforma experimenten och utföra analyserna med ANOVA. Om du har tid rekommenderar vi alltså att du bekantar dig med innehållet i även dessa kapitel.

I korthet kan man säga att kapitel 11 rekapitulerar mycket av det som sagts i tidigare avsnitt. En viktig och användbar nyhet är att kapitlet ger ett verktyg för att utveckla experiment med ett i stort sett obegränsat antal nestade och ortogonala faktorer (stycke 11.3 och 11.4). Som diskuterades tidigare (kapitel 10) kräver inte detta en fullständig förståelse för algebraiska härledningar. Vi rekommenderar dock den procedur som beskrivs under rubriken General method to determine the variance components estimated by MS i Statcomp_3v4.pdf före den som finns i kursbokens sektion 11.4. Med hjälp av datorn kan man enkelt få fram vad medelkvadratsummorna skattar genom att använda funktionen estimates(object) i programpaketet GAD för r. En annan intressant diskussion i detta kapitel rör problem som uppstår då data saknas och man har s.k. obalanserade designs (stycke 11.10).

De båda huvudexemplen i kapitlet finns här med hela datauppsättningar, analyser och tolkningar.

Medan kapitel 11 syftar till att ge kunskap om generella regler för att utföra olika typer av ANOVA, syftar kapitel 12 till att ge specifik kunskap om olika specialfall av ANOVA. Begrepp som "randomised blocks", "split-plot", "latin squares", "repeated measures" och "asymmetrical designs" är begrepp som man då och då stöter på i litteraturen. Bortsett från den senare typen är AJU inte någon förespråkare för dessa typer av experiment. Man kan förmodligen säga att boken på ett kritiskt sätt illustrerar de problem som finns med dessa uppställningar, men kanske inte poängterar de eventuella fördelarna. Om man vill få en mer positiv bild skall man nog konsultera någon annan textbok eller artikel. Å andra sidan finns det teoretisk och viss empirisk substans i de invändningar som framförs och man bör undersöka dessa innan man planerar experiment efter dessa riktlinjer.

När det gäller asymmetriska uppställningar är AJU å andra en av de mest ivriga förespråkarna. Dessa är besläktade med s.k. kontraster (a priori jämförelser) som används för att göra vissa specifika jämförelser (jämför a posteriori jämförelser som specificeras efter ett inledande F-test). Utvecklandet av asymmetriska designs för att undersöka antropogena effekter på miljön har varit ett av de forskningsfält där AJU har varit mest aktiv. Den stora fördelen med dessa är att de kan användas för att upptäcka störningar även i situationer när det endast finns en påverkad lokal men ett antal möjliga kontroll-lokaler.

Kursboken behandlar inte multivariat statistik, men det är viktigt att du förstår skillnaden mellan multifaktoriell och multivariat. Som vi sett har vi en multifaktoriell situation när flera faktorer(t.ex. PCB-koncentration och temperatur) påverkar en variabel (t.ex. tillväxt), som vi mäter på ett stickprov av individer. En multivariat situation har vi när vi mäter flera variabler (t.ex. tillväxt, halten av ett hormon och antal missbildningar av en speciell typ) samtidigt på alla individerna i stickprovet, för att se om de påverkas av en eller flera faktorer.

Observera att det som i ett experiment är faktor kan i ett annat vara mätvariabel och tvärt om. Det beror på de förklaringsmodeller man vill undersöka.

Repetition

Mycket bra repetition får du om du läser avsnittet ANOVA with two orthogonal factors på sidorna 16 - 20 i Statcomp_3v4.pdf!

Övningar

De obligatoriska övningarna, som ingår i examinationen finns här.

Nyckelord

faktoriellt experiment, ortogonal faktor, interaktion, samspel, huvudfaktor