Avsnitt 8 Regression

Sammanfattning av innehåll

Detta avsnitt handlar om metoder för att analysera samband mellan två variabler. Låt säga att vi är arbetar i ett projekt där man försöker avhjälpa problem med övergödning och planktonblommningar genom att plantera in blåmusslor som filtrerar bort växtplankton. I det sammanhanget kan det vara intressant att undersöka hur musslornas filtrerhastighet (antal liter havsvatten per timme) varierar med musslornas storlek (skallängd eller köttvikt). Ett sätt att gå till väga vore att mäta filtrerhastigheten hos ett antal små, medelstora och stora musslor, och sedan testa om medelvärdena skiljer sig (med ANOVA). Ett bättre sätt vore att försöka beskriva sambandet mellan de två variablerna mer i detalj. Den enklaste modellen för ett samband mellan två variabler är ett linjärt samband enligt: y = bx + a, där y=filtrerhastighet, x=skallängd, a=interceptet (värdet på y när x=0) samt b=linjens lutningskoefficient.

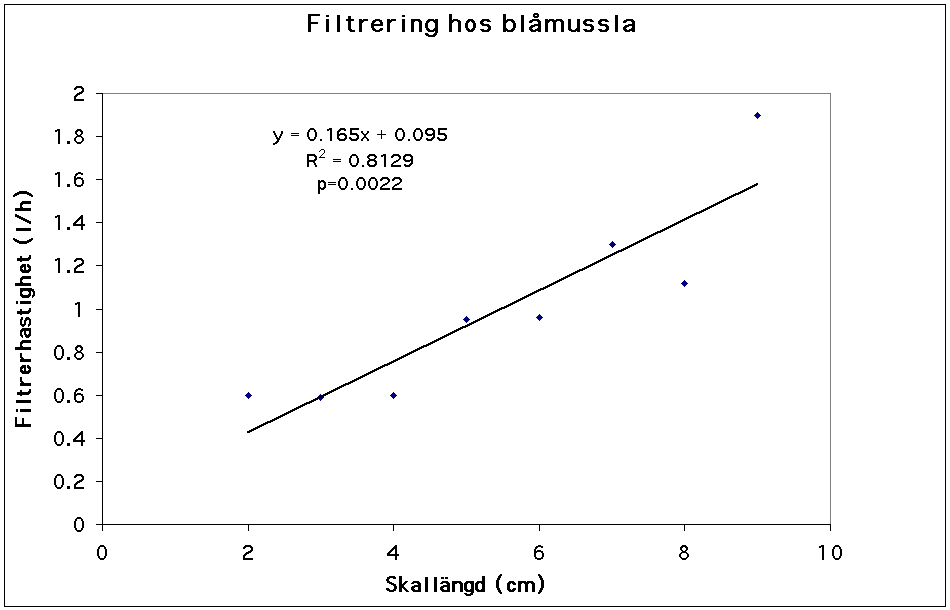
a och b är sanna populationsparametrar som skattas av a och b. Linjen anpassas till de olika mätpunkterna så att avståndet mellan punkterna och linjen blir så litet som möjligt. Nollhypotesen om sambandet är att b=0. Sannolikheten, p, att få b=0.165 (se figur) givet att b=0 kan undersökas med ett t-test eller F-test. P-värdet blev 0.0022 vilket betyder att vi förkastar nollhypotesen, och konstaterar att det finns ett (positivt) samband mellan storlek och filtrerhastighet. Eftersom punkterna är ganska spridda kring linjen så drar vi också slutsatsen att andra faktorer än skallängd påverkar filtrerhastigheten. Denna oförklarade variation, residualvariationen, kan vara slumpmässig variation eller variation orsakad av andra (okända) faktorer. Hur mycket av variationen i filtrerhastighet som förklaras av just skallängd skattas med determinationskoefficienten, R².

När man presenterar resultat från en regressionsanalys, tex i en figur, så bör det alltid finnas med information om:

1. Sambandets ekvation y=bx+a

2. Sambandets styrka R²

3. Sambandets signifikans p-värdet

Regressionsanalys används också ofta när man vill göra FÖRUTSÄGELSER om y utifrån x. Tex i spektrofotometrar där absorbansen (som är lätt att mäta) har ett starkt samband med koncentrationen av något ämne som i sig är svårt att mäta.

I kapitel 13 i boken så är delkapitel 13.1 -13.5 mest väsentligt för den här kursen. Ni behöver dock inte kunna formlerna för att beräkna parametrarna. t-test är vanligast när man testar ett samband; t-test avänds också om H₀ är annan än b=0 (tex b=0.1).

13.6 - 13.15 ligger utanför kursen och behandlas endast kort nedan.

Antaganden:

För regressionstest gäller samma typ av antanganden som för ANOVA:

1. Den oberoende variabeln skall vara "fixed"; det skall inte finnas någon variation associerad med de olika "nivåerna" på den oberoende variabeln. Detta kallas att "x är mätt utan fel". Om den oberoende variabeln är "random" så skall ett annat test användas: sk regression model 2 eller korrelationstest (se nedan)

2. För varje värde på x så är y normalfördelad

3. För varje värde på x så är variansen i y lika stor (homogen)

4. Observationerna skall vara oberoende

Anagande 1 och 4 faller på utföraren att tillgodose medan 2 och 3 kan testas. Problemet är att man ofta endast har en observation av y per värde på x. Det man kan göra är att rita en graf på residualerna; om antagande 2 och 3 är uppfyllda så bör dessa vara normalt fördelade kring noll.

Regression i Excel

Regression kan göras på (minst) två sätt i Excel. Vi använder exemplet med musslorna:

Skallängd	Filtrerhastighet
2	0.6
3	0.59
4	0.6
5	0.95
6	0.96
7	1.3
8	1.12
9	1.9

Välj "infoga diagram" eller klicka på diagramguiden. Klicka på punktdiagram och följ guiden. När diagrammet är färdigritat klickar du på någon av punkterna varvid alla (eller de flesta) punkter ändrar färg. Sedan går du in diagrammenyn och väljer "infoga trendlinje". Här kan du välja vilken typ av regression du vill göra. Välj "linjär". Sedan klickar du på fliken "Alternativ" och klickar i "visa ekvation" och "visa R²", sedan trycker du OK. Nu visas linjen, ekvationen och R². Tyvärr får man inte p-värdet här.

För det statistiska testet av lutningskoefficienten måste man använda funktionen "Dataanalys" under "Verktyg". Välj regression, och markera sedan indata och utdataområde. Om du vill att denna modul skall göra ett diagram av regressionen eller av residualerna så måste du välja ett nytt arbetsblad eller en ny arbetsbok som utdataområde, annars får du felmeddelandet: "diagram kan inte göras i en delad arbetsbok". Detta är troligen en bug.

I utdataområdet så erhålles bla följande:

Regression Statistics
Multiple R	0.902
R Square	0.812
Adjusted R Square	0.781
Standard Error	0.209
Observations	8

	Coefficients	Standard Error	t Stat	P-value
intercept	0.095	0.19251	0.4934	0.639
lutningskoefficient	0.165	0.0323	5.106	0.0022

R Square är samma R² som i figuren. Koefficienterna är a och b. Dessa åtföljs av standard errors, t och p-värden. P-värdet gäller H₀ att koefficienten är lika med 0.

Notera att Multiple R är korrelationskoefficienten R som är ett mått på styrkan i sambandet.

Angränsande termer och teman:

Icke-linjär regression. Den enklaste modellen för ett samband är ett linjärt samband. Ofta är samband mera komplicerade, och ibland finns det logiska modeller för dessa. Tex så är det INTE troligt att sambandet mellan filtrerhastighet och skallängd hos blåmussla är linjärt, eftersom födoupptagsapparaten troligtvis snarare ökar med volymen på musslan. Prova att anpassa en annan model med hjälp av excel och se om ni får ett högre R²-värde.

Multipel regression används när man vill undersöka den relativa förklaringsgraden av flera olika oberoende variabler. Tex betydelsen av flera olika fettsyror i kosten för tillväxt hos grisar.

Kovariansanalys används för när man vill kompensera för en variabel i ANOVA. Tex om man vill testa skillnad i PCB hos sill från olika områden så kan man kompensera för att fetthalten varierar mellan individuella fiskar (se ytterliggare exempel i kursboken).

Korrelation används när man vill beskriva graden av association mellan två variabler. Uttrycks som korrelationskoefficienten R.

Regression Modell 2 används när det finns ett kausalt samband, men båda variablerna är att betrakta som "random".

Nyckelord

regression, korrelation, samband

Förslag på fördjupning

Hampton, R. 1994. Biological Statistics. WCB Publishers. ISBN 0-697-20209-7. Bra och lättfattlig introduktion till beskrivande statistik, ANOVA och regression.

Sokal, R.R., Rohlf, F.J. 1995. "Biometry, 3rd edition." Freeman and Company, New York. Klassisk och innehållsrik lärobok i statistik med biologiska exempel. Innehåller bla. Model 2 regression, multipel regression, icke-linjär regression och kovariansanalys.