Avsnitt 6 Hierarkisk design

I detta kapitel beskrivs sk hierarkiska experimentuppställningar. Detta är första gången på kursen då vi stöter på experiment med mer än en faktor. Förutom den faktor som vi huvudsakligen är intresserade av (effekten av pollinatörer, som i boken, eller effekten av salthalt, temperatur, PCB, predation etc.) innhåller hierarkiska uppställningar även s.k. "nestade" faktorer som har med experimentets praktiska omständigheter att göra ("nestad" är en försvenskning av engelskans "nested", som betyder ungefär att faktorn är innesluten i en annan faktor).

Läs kursbokavsnitten 9.1 och 9.2 och forsätt sedan med sammanfattningen här nedan.

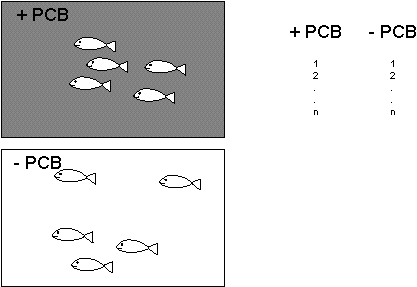
I boken introduceras nestade faktorer med hjälp av ett "skräckexempel" (exemplet med pollinatörer på s. 243-244) som visar på problem som uppstår om man inte använder nestade faktorer. Ett liknande exempel skulle kunna vara om man vill undersöka effekten av PCB på tillväxten av fiskar i ett akvarieexperiment. För att göra detta tillsätts PCB till ett akvarium med 5 fiskar. Till ett kontrollakvarium med 5 andra fiskar tillsätts inget PCB (se figur 1). Efter en viss tid mäter man tillväxten hos varje fisk. Problemet med detta är att om man finner en skillnad i tillväxt mellan fiskar som varit i akvariet med PCB och dem som varit i kontrollakvariet, kan man inte veta om det beror på att man tillsatt PCB eller om det beror på att något annat har skilt sig mellan akvarier. Akvarierna har stått på olika platser, ett av akvarierna kan har varit kontaminerat, eller en fisk i ena akvariet har varit aggressiv, sjuk eller konstig på något sätt som även påverkat de andra fiskarna som var i samma akvarium. Man kan säga att effekten av PCB kan vara sammanblandad ("confounded") med andra, okända faktorer. Det faktum att man har 5 fiskar spelar ingen roll eftersom fiskarna inta kan anses vara oberoende. En vanlig benämning på sådana icke-oberoende "replikat" är "pseudoreplikat".

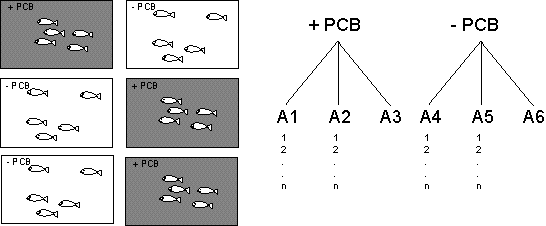
En lösning på detta problem är att inse att det är akvarierna som är den egentliga replikationsenheten och att därför ha flera akvarier för varje behandling (+PCB och - PCB; se figur 2). I ett sådant experiment har man alltså två faktorer: (1) Behandling och (2) Akvarium. Akvarium är i detta fall en "nestad" faktor. Detta innebär att varje varje nivå av den första faktorn (d.v.s. + eller - PCB) har unika nivåer av faktorn "Akvarium". I figuren nedan kan vi se att A1, A2 och A3 finns bara i behandlingen + PCB, medan A4, A5 och A6 finns bara i behandlingen - PCB. Sådana nestade faktorer skrivs "Akvarium (Behandling)". Man säger att "akvarier är nestade i behandling".

Ett mer tekniskt sätt att se på saken är att man har nu har tre olika "saker" som orsakar variation i tillväxt mellan fiskar (stycke 9.3). ANOVA kan på ett enkelt sätt användas för att skatta storleken och betydelsen av dessa variationskällor: (1) mellan fiskar inom akvarier, (2) mellan akvarier inom behandlingar och (3) mellan behandlingar. ANOVA kan dessutom användas för att testa hypoteser om signifikanta skillnader (1) mellan akvarier och (2) mellan behandlingar. Studera noga figurerna 9.2 och 9.3 så att du förstår innebörden av dessa hypoteser.

De tekniska detaljerna om hur man beräknar de olika varianserna och hur man går till väga för att testa hypoteserna beskrivs i stycke 9.4 och 9.5. Tabell 9.3 sammanfattar strukturen och komponenterna i en nestad ANOVA. Om vi vill konkretisera exemplet kan vi säga att "Among treatments" är Behandling (+ / - PCB), "Among units" är Akvarier och "Within samples" är inom akvarier mellan fiskar. Som vanligt med ANOVA-tabeller finns kolumner för kvadrerade avvikelser (Sum of squares, =SS), frihetsgrader (df) och variansskattningar (Mean squares, =MS). Studera tabellen och försök förstå vad de olika sakerna är. Till exempel: SST är summan av den kvadrerade avvikelsen av varje enskilt värde från medelvärdet av alla värden. Hur kan man i ord uttrycka SSW, SSB(A) osv? För att beräkna varianser (MS) måste sedan SS divideras med antalet frihetsgrader. Dessutom finns i kolumnen längst till höger ("Mean square estimates") information om vilka "varianskomponenter" som ingår i variansskattningarna. Att förstå exakt varför de olika faktorerna innehåller just dessa komponenter kan vara lite svårt. Häng inte upp er på detta nu: vi kommer att lära oss regler för hur man kan göra detta senare. Det viktiga just nu är att veta att flera varianskomponenter ingår i MS-skattningarna och att detta har en stor betydelse när man bestämmer hur man skall konstruera test-statistikan (detta diskuteras i stycke 9.6.1). Kärnan i resonemanget är dock att man alltid vill konstruera en F-kvot som i nämnaren innehåller allt som finns i täljaren, förutom den faktor som man vill testa. Till exempel: om vi vill testa om det finns en signifikant variation mellan akvarier dividerar vi MSB(A) med MSW. Som du ser i kolumnen längst till höger innehåller MSW endast (sigma)²_e, medan MSB(A) innehåller (sigma)²_e plus n gånger (sigma)²_B(A). Om koten mellan dessa är signifikant större än 1 måste alltså (sigma)²_B(A) vara skild från noll. Med ett liknande resonemang kan vi bestämma hur man skall bilda en F-kvot för faktorn Behandling. Att förstå varför F-kvoterna konstrueras som de gör är viktigt att förstå när det blir fråga om mer komplicerade experiment.

Försäkra dig nu, innan du läser vidare, om att du förstår allt i avsnitten 9.1 t.o.m. 9.6.3, inklusive tabeller och figurer. Det du inte måste kunna är matematiken för att härleda de "varianskomponenter" som ingår i variansskattningarna.

Nu ska du alltså både förstå logiken bakom nestad variansanalys och varför denna typ av faktor är nödvändig i många experimentutformningar. Dessutom ska du kunna utföra alla beräkningar. Alla steg måste du behärska! Tag hjälp av de räknade exemplen och övningsuppgifterna, och be om hjälp när du inser att du behöver det. Titta först på uträkningarna som hör till tabellerna 9.1, 9.4 and 9.5 i Exempel på sidan 243 om variation i fertilitet och fruktproduktion.xlsx. Dubbelklicka i enskilda celler för att se formler och hänvisningar markerade med olika färger.

Funktionen KVADAVV beräknar alltså kvadratsummor (Sums of Squares, SS). Jämför med Sums of Squares i kursbokens tabell 9.3.