Sammanfattning av innehåll

Kapitel 6: Simple experiments comparing the means of two populations (6 - 6.6 och 6.9)

I kapitel 6 används några enkla experiment som exempel för att illustrera användbarhet och begränsningar med s.k. t-test. Vi har tidigare stött på teststatistikan t när det gällde att konstruera konfidensintervall för medelvärden men den används också ofta för att testa om medelvärden skiljer sig mellan TVÅ olika grupper.

Kapitlet inleds med några exempel med s.k. parade t-test. Dessa används ibland i situationer när man har mätningar vid två tillfällen på samma statistiska individ (t.ex. en mussla, mus eller provruta). AJU menar att parade t-test kan vara lämpliga i experiment där det inte finns någon ambition att utreda orsakssammanhang. Han menar dock att dessa test oftast är olämpliga och föreslår att experimenten planeras för analys med oparade t-test eller andra metoder som diskuteras senare i boken.

Det huvudsakliga problemet med parade t-test är att effekten av den process man vill uttala sig om ofta (alltid?) löper risken att bli sammanblandad ("confounded") med effekten av andra processer. Ett tydligt exempel på detta är försöket med musen som injiceras med en drog (s. 105 - 106). Förutom drogen utsätts musen för olika typer av hantering som också riskerar att påverka dess fysiologi på ett oförutsägbart sätt. För att utvärdera betydelsen av sådana effekter behövs olika typer av kontroller på den experimentella proceduren. Detta kan inte på ett enkelt sätt göras med hjälp av parade t-test.
 
 

Ett viktigt tema i kapitlet är förhållandet mellan den logiska hypotesen och det statistiska testet. För det första beskrivs situationer där statistiskt korrekta test kan leda till logiskt felaktiga slutsatser. Detta kan uppträda då den effekten av den aktuella processen är sammanblandad men en annan okänd process eller om experimentets utgångspopulation inte motsvarar den som specificerats av hypotesen. En annan situation där relationen mellan statistiska slutsatser och biologiska hypoteser behöver beaktas är när den statistiska noll-hypotesen förkastas men resultatet inte kan förklara den ursprungliga kvantitativa observationen. I sådan fall rekommenderas att hypotesen görs så specifik som möjligt.
 
 

Ett exempel på specificering av hypoteser ges i stycke 6.9.2 där ett experiment med fåglar som äter ödlor och där det finns en kontroll på den experimentella proceduren. Med detta exempel illustreras ett problem med t-test som uppstår på grund av att dessa bara kan användas för att jämföra två grupper. För att testa hypotesen krävs flera separata test. Detta ökar risken för typ 1-fel om inte en s.k. Bonferroni-korrektion görs. Å andra sidan leder sådana korrektioner till att risken ökar att man inte upptäcker sanna skillnader i medelvärden (detta diskuteras utförligare i stycke 8.6.2).
 
 

Kapitlet innehåller också diskussioner kring varianshomogenitet, F - fördelningens ursprung, statistisk styrka och några alternativa statistiska metoder. Dessa ämnen kommer vi att återkomma till och diskutera mer utförligt i senare kapitlet.
 
 

Kap 7 Analysis of variance. 7.1-7.19

Variansanalys (ANOVA) är en kraftfull metod för att utvärdera experiment. Till skillnad från vad namnet antyder så används metoden för att undersöka skillnader mellan medelvärden. Namnet kommer ifrån det faktum att man använder analyser - skattningar - av just varianser för att sluta sig till egenskaper hos medelvärden. Samband mellan medelvärden och varianser hos stickprov och populationer beskrivs av stickprovs-teori (kap 5). Stycke 7.5-7.7 beskriver algebraiskt bakgrunden till ANOVA. Ett alternativt sätt att betrakta detta kan illustreras med ett exempel:
 
 

Anta att ni vill undersöka om det är någon skillnad mellan medelvärden i tre (a) olika populationer. Nollhypotesen blir då H₀:µ1=µ2=µ3. Från respektive population tar ni ett stickprov av storleken (n) och beräknar sedan medelvärdena xbar1, xbar2 och xbar3 [redan här kan man ana att om ni beräknade konfidensintervallet kring vart och ett av medelvärdena så skulle ni kunna bilda er uppfattning om H₀]. Varje stickprov ger också skattningar av populationernas varianser: s²₁, s²₂, s²₃. Anta nu att dessa tre populationers sanna varianser är lika stora, dvs σ²₁ =σ²₂=σ²₃ = σ²_e. [Det lilla e:et kommer från engelskans error, i betydelsen avvikelse; varians beskriver ju enskilda värdens (kvadrerade) avvikelse från medelvärdet]. Vi har nu tre lika goda skattningar av σ²_e, och för att få en enda skattning tar vi medelvärdet av dessa tre: (s²₁+s²₂+s²₃ )/a = s²_e. Denna varians, s²_e, skattar σ²_e och beräknas som MS_inom (se formeln i tabell 7.6.). [MS_inom kallas ibland för MS_within, MS_error eller MS_residual].
 
 

Om H₀ (µ1=µ2=µ3) är sann så skattar xbar₁, xbar₂ och xbar₃ samma medelvärde. Dessa tre skattningar är inte identiska; hur mycket olika skattningar av samma medelvärde varierar bestämms av n och σ²_e enligt förhållandet σ²_xbar = σ²_e / n (se handledning kap 5). Alltså: om H₀ är sann så kommer n * s²_xbar att skatta σ²_e. Detta beräknas som MS_mellan [MS_mellan kallas ibland för MS_among, MS_between eller MS_treatment].
 
 

Om H₀ är sann så kommer MS_inom och MS _mellan alltså att skatta samma sak (σ²_e). Den förväntade kvoten mellan dessa variansskattningar, F = MS_mellan /MS_inom är därmed 1. Om däremot H₀ är falsk så kommer medelvärdena att skilja sig mer än man kan förvänta av slumpen, MS_mellan kommer att vara större, och kvoten, F kommer att bli större än 1. Hur mycket större än 1 som F måste vara för att vi skall förkasta H₀ bestämmer vi sjäva; vanligt är att det skall vara mindre än 5 % sannolikhet att få ett så stort F som vi fick, eller större, givet att H₀ är sann.
 
 

För att ovanstående resonemang skall gälla får inte varianserna i de tre populationerna vara olika. Vidare så bör de ingående värdena i MS_mellan och MS_inom vara normalfördelade; medelvärdena i MS_mellan kan antas vara normalfördelade, enligt centrala gränsvärdessatsen; huruvida de tre populationerna är normalfördelade är ofta svårt att kolla, särskilt om stickprovsstorleken är liten. Datorsimuleringar antyder dock att avvikelser från normalfördelning vanligtvis har liten betydelse, särskilt om stickprovsstorleken inte är liten.
 
 

Antagandet om lika (homogena) varianser skall testas innan man använder ANOVA. Det finns olika tester för detta. AJU förordar Cochrans test där man testar om någon av de skattade varianserna är mycket större än de övriga varianserna. Det kritiska värdet för statistikan C finns tabulerad i en Excel-fil, som går att ladda ner från sidan med tabeller. Ett alternativ för att utföra Cochrans test är att använda C.test(object) i R-paket GAD. Om varianserna visar sig vara olika (heterogena) kan man ibland avhjälpa detta genom att transformera originaldata.
 
 

Oberoende data betyder, som namnet säger, att enskilda värden eller observationer skall vara oberoende från varandra. Det betyder också att olika behandlingar skall vara oberoende av varandra. Stycke 7.14 om oberoende är särskilt viktigt eftersom det inte behandlas särskilt utförligt i statistikböcker, ofta är svårt att testa oberoende, och att det faller på er som biologer att genom noggrann eftertanke och planering försäkra er om att data är oberoende. Etablering av oberoende är en stor och viktig del av experimentplanering! Att bryta mot oberoende benäms på engelska med termen "confounding": Man tror att man testar en sak när man i själva verket testar en annan. Att undvika confounding är nödvändigt vid alla typer av experiment och statistiska test inte bara ANOVA [se ovan, kap 6].  

Studera nu det genomarbetade exemplet Underwood tabell 7.1. Exempel på variansanalys med SNK test. Det som är längst ner i filen om A posteriori-test (SNK) kan du vänta med tills du har läst kapitel 8. Det samma gäller fliken Styrka fixerad faktor.
 
 

Kap 8 More analysis of variance; ej 8.3-4.

När man med variansanalys undersöker betydelsen av en faktor, tex mängd mat, för en variabel, tex tillväxthastighet, så säger man att faktorn föda har olika nivåer ("levels"); ingen mat, lite mat och mycket mat är exempel på tre nivåer. I manupulativa experiment kallas nivåerna för behandlingar ("treatments"). Hur dessa nivåer väljs beror givetvis på hur modellen och hypotesen är är formulerad. Det finns dock två principiellt olika sätt att välja nivåer för en faktor:
 
 

"Random factor" där nivåerna är slumpmässigt valda bland en stor mängd olika, möjliga nivåer. Nivåerna anses "representera" faktorn, och modell och hypotes gör förutsägelser om faktorn påverkar responsvariabeln. T. ex. om temperaturen har betydelse för tillväxthastigheten.
 
 

"Fixed factor" har endast vissa specifika, av modellen bestämda, nivåer. T. ex. om modellen säger att en viss fettsyra är nödvändig för tillväxt så måste det finnas en behandling med denna fettsyra och en behandling utan (kontroll).
 
 

Att kunna skilja på fixed och random factors är viktigt eftersom det har betydelse för tolkningen av resultaten. Det har också en viktig teknisk betydelse eftersom det bestämmer hur F-kvoten skall konstrueras när man testar flera faktorer samtidigt (två-, eller flerfaktors ANOVA; kap 10).
 
 

I en variansanalys testar man nollhypoteser av typen H₀:µ1=µ2=µ3. Om de stickprovsmedelvärden man erhållit i experimentet är mer skilda åt än man kan förvänta sig av slumpen, dvs om F är större än man kan förvänta sig av slumpskäl, så tror vi inte på H₀; vi förkastar H₀. Den statistiska analysen tar dock inte slut här: Om den faktor vi undersöker är att betrakta som en sk fixed faktor så måste vi ta reda på vilka av de alternativa hypoteserna som givit rätt förutsägelser, dvs vilka av de tre (eller flera) medelvärdena som skiljer sig från varandra. Antingen är vi endast intresserade av några specifika, i förväg bestämda, jämförelser (a priori kontraster) eller så gör vi alla möjliga parvisa jämförelser av medelvärden (a posteriori "multiple comparisons"). Det senare är vanligast. I datorprogram finns det ofta flera olika varianter på a posteriori-test. I grunden är alla dessa test varianter på parvisa t-test. AJU förordar ett test som kallas SNK.  

Studera Underwood tabell 7.1. Exempel på variansanalys med SNK test och 3. Exempel med predation på sidan 227 och i tabell 8.5a.xlsx  

Om den undersökta faktorn är att betrakta som "random" så behöver man inte gå vidare och undersöka vilka medelvärden som skiljer sig, eftersom hypotesen gäller faktorn som sådan, och inte de enskilda (slumpmässigt valda) nivåerna.
 
 

Sammanfattning av innehåll

Avsnitt 5: Statistisk styrka samt alternativa metoder (5.11-5.13 (repetition), 6.7-6.8, 8.3-8.5 )

Detta avsnitt har två teman: dels har vi samlat det i boken som rör statistisk styrka för enfaktorsdesign, och dels det som rör statistiska test som alternativ till ANOVA.

Begreppet statistisk styrka ("power") är fundamentalt inom experimentplanering. Power i ett experiment beskriver möjligheten att upptäcka en skillnad mellan behandlingar - när en sådan skillnad verkligen existerar. Det finns två typer av misstag man kan göra när man med hjälp av statistik utvärderar biologiska experiment. Detta gäller både statistik och logik (se tabell).

Feltabell

	H0 Sann	H0 Falsk
Acceptera H0	Korrekt; =1-α	Typ 2-fel; =β
Förkasta H0	Typ 1-fel; = α	Korrekt; =Power =1-β

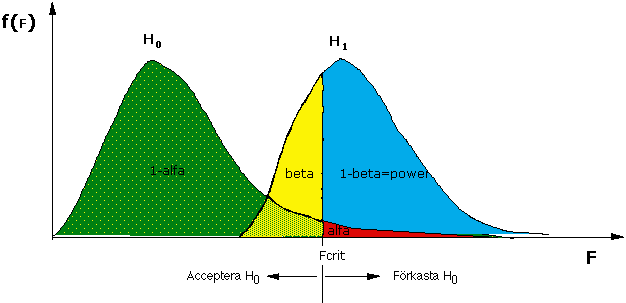
Dels finns risken att man förkastar en sann nollhypotes. Sannolikheten för att göra detta har man dock bestämt i förväg (oftast 5 %). Detta misstag kallas typ-1 fel eller α-fel (se figur). F i figuren är, liksom t, exempel på en teststatistika.

Gör man inte en analys av statistisk styrka före experimentet är sannolikheten att man skall göra ett typ-2 fel okänd, men om man gör power-analysen, så vet man hur stort experimentet behöver vara för att risken för typ-2 fel ska vara tillräckligt liten. Finns en verklig skillnad, så är den statistiska styrkan (1-β) lika med sannolikheten att förkasta en falsk nollhypotes.

I figuren kan man se att sannolikheten för typ 1 och typ 2 fel är beroende av varandra: Om vi minskar α (t.ex. α = 0.01 i stället för 0.05) så ökar Fcrit och därmed samtidigt β. Avvägningen mellan α och β bör ske med hänsyn till kostnaden av att begå det ena eller andra misstaget.

För att kunna beräkna β och power måste man känna till hur teststatistikan (t eller F) fördelar sig när H₀ är falsk. När H₀ är sann så fördelar sig F kring 1, men när H₀ är falsk så fördelar sig F kring ett värde större än 1. Fördelningen av teststatistikan beror på:

1. Skillnaden mellan medelvärdena, effektstorlek	A
2. Storleken på variansen	σ2e
3. Storleken på α	α
4. Antalet replikat	n

Av detta följer att vi i förväg kan beräkna hur många replikat vi behöver (= pengar och/eller tid) för att kunna, med en viss sannolikhet, detektera en viss specifierad skillnad mellan behandlingar, under förutsättning att vi har en bra skattning av variansen.

Fördelningen av F när H₀ är falsk beräknas på olika sätt för faktorer som är fixerade och slumpmässiga. För fixerade faktorer har F under H₁ en sk "icke central" fördelning, och betecknas med Φ. β och power kan man få från en Φ-tabell, men de kan också beräknas i Excel. Se Statistisk-styrka-stickprovsstorlek-fixerad-alt-slumpm-faktor.xlsx. För slumpmässiga faktorer så fördelar sig F under H₁ som F/(1+ nσ²_A /σ²_e) varför man kan använda den centrala F fördelningen för att beräkna β och power.

Alternativa metoder: Om antagandena för parametriska tester (t-test, ANOVA) inte är uppfyllda så används ibland andra, alternativa, statistiska tester som inte bygger på dessa antaganden (sk. icke-parametriska tester). Icke-parametriska tester har dock ofta en lägre power än parametriska test eftersom de endast tar hänsyn till rankordningen av data och inte magnitud i skillnader. Det är också ofta förbisett att även vissa icke-paratriska test bygger på antaganden som måste uppfyllas för att man skall kunna lita på testet.

Nyckelord

t-test (parat och oparat), "confounding" (=sammanblandning), kontroll, Bonferroni-korrektion, ANOVA, balanserad stickprovsstorlek, "Sum of Squares", SS, "Mean square", MS, F - kvot, antagande för ANOVA, oberoende data, homogena varianser, normalfördelning, transformering, Cochrans test, "fixed" och "random" faktorer, "Multiple-comparison test", statistisk styrka, power, typ-1 fel, typ-2 fel, α, β, effekt-storlek (A).  

Nu förväntas du alltså både förstå logiken bakom enfaktors variansanalys och analys av statistisk styrka. Dessutom ska du kunna utföra alla beräkningar. Alla steg måste du behärska! Tag hjälp av de räknade exemplen och övningsuppgifterna, och be om hjälp när du inser att du behöver det.
 
 

Lösta exempel

Studera nu alla dessa genomarbetade exempel från kursboken!
 
 

Övningsuppgifter
Det är bra att göra många övningsuppgifter. Här finns en tidigare uppsättning med nyttiga övningsuppgifter. Gör dem gärna! Här finns de nyare uppsättningarna med obligatoriska uppgifter till kapitel 6, kapitel 7 och kapitel 8. Observera att vi förutsätter att du gör alla de nyare övningsuppgifterna, även om du inte behöver redovisa dem alla i examinationen.