|
Hypotestestning (kap 4, 5) |
Sammanfattning av innehåll
Kapitel 4: Statistical tests of null hypotheses
Inom det vetenskapliga arbetssätt som redogjordes för i kapitel 1 var test av hypoteser en avgörande komponent. De exempel som redovisades där var av karaktären antingen eller. Hypotesen (och modellen) kunde förkastas med en observation. Oftast är det dock så att experiment har många möjliga utfall. I sådana fall behövs statistiska test för att avgöra om utfallet stöder hypotesen och modellen. Detta kapitel handlar om vilka steg som behövs för att ett statistiskt test skall kunna användas för att förkasta eller finna stöd för en hypotes. Dessa steg är desamma oavsett om det statistiska testet utgörs av ANOVA, t-test eller någon annan teknik.
Förutsättningen för ett meningsfullt statistiskt test är som beskrivits tidigare att man definierat observationen som skall förklaras och tydligt formulerat sin modell, hypotes och noll-hypotes. För att ett statistiskt test skall kunna utföras måste sedan den logiska noll-hypotesen översättas till en statistisk noll-hypotes (H0). Detta låter kanske komplicerat men vad det handlar om är att definiera en frekvensfördelning av utfall som gäller om noll-hypotesen är sann.
För att göra detta måste vi först bestämma oss för en s.k. test-statistika. Denna är en mätbar variabel som väljs så att man på teoretisk väg exakt vet sannolikheten att den skall vara ett visst värde om H0 är sann. Dessa sannolikheter kan man ofta finna i tabeller men numera kan man också ta reda på många av dessa i olika kalkylprogram som exempelvis Excel. Exempel på sådana statistikor är F, t och Z.
Nästa steg är att bestämma hur osannolikt ett utfall skall vara för att vi ska betraktya det som osannolikt att H0 är sann, d.v.s. att hypotesen därmed är sann! Gränsen för vad som anses osannolikt sätts ofta i dessa sammanhang till 1 på 20 (5 %). Detta är endast en konvention. Denna diskuteras senare i boken. När vi bestämt vad vi anser som osannolikt kan vi med hjälp av den kända fördelningen av statistikan bestämma hur stor eller liten den observerade statistikan (i det kommande experimentet) måste vara för att vi skall betrakta det som osannolikt att H0 gäller. Värdet på statistikan när utfallet övergår från att vara sannolikt till osannolikt kallas för statistikans "kritiska värde".
Därefter är det dags att utföra det tänkta experimentet och beräkna värdet på den observerade statistikan. Om värdet faller utanför vad som anses sannolikt om H0 är sann, drar vi slutsatsen att hypotesen var sann och vi kan börja fundera över nya hypoteser. Notera dock att det alltid är möjligt att experimentet resulterar i ett ovanligt utfall trots att noll-hypotesen är sann. Denna sannolikhet har vi ovan satt till 5 %. Således finns det en risk att vi begår ett misstag när vi drar en slutsats från vårt experiment. Denna typ av misstag, att felaktigt förkasta H0 kallas typ 1-fel.
Studera nu Exempel med kast med krona 10 gånger sid 51 fig 4.1.xlsx.
Kapitel 5: Statistical tests on samples, fram till kap 5.10
Som vi diskuterat tidigare kan vi med hjälp av stickprov göra skattningar av populationers frekvensfördelningar. Vi förutsätter då att stickproven är representativa. Men hur vet vi hur väl stickprovets medelvärde tex, liknar eller skattar populationens medelvärde?
Om vi gör tankeexperimentet att vi tar TVÅ olika stickprov från en population, så kommer dessa två stickprovs medelvärden givetvis inte att vara helt identiska; ej heller förefaller det troligt att något, eller båda, medelvärdena kommer att vara helt identiska med populationens medelvärde. Antar vi att variabeln mäts utan systematiskt fel, kan vi fråga oss hur mycket upprepade stickprovsmedelvärden liknar varandra och därmed liknar populationens medelvärde. Desto närmare skattningen från stickprovet ligger det sanna värdet hos populationen, desto bättre precision har vi. Precisionen beror på två saker: stickprovets storlek (n) samt populationens varians. Medelvärden baserade på ett litet stickprov draget från en population med en stor varians är oprecisa - vilket känns logiskt. Kan vi skatta precisionen? Ja, det kan vi! Vi vet ju vår stickprovsstorlek och populationens varians (σ2) skattar vi utifrån stickprovet (s2).
Precisionen för ett skattat medelvärde kallas standard error, och är i själva verket standardavvikelsen för oändligt många stickrovsmedelvärden. Denna standardavvikelse, d.v.s. medelvärdets medelavvikelse, kan dock skattas från ett enda stickprov: se = standardavikelsen för stickprovet (s) dividerat med roten ur stickprovsstorleken (n). Om standard error är stort så är stickprovets skattning av populationens medelvärde osäker. Hur säker skattningen är kan vi ta reda på. Vi kan räkna ut ett intervall kring xbar inom vilket vi känner oss relativt säkra att populationens medelvärde finns. Intervallet kallas konfidensintervall (CI) och bygger på det faktum att medelvärden tenderar att vara normalfördelade. Om vi tex vill vara 95 % säkra att µ finns inom intervallet så blir CI(0.95) = xbar ± 1.96*se (1.96 kommer från att 95 % av en normalfördelning innesluts av 1.96 * s(xbar)); talet 1.96 förutsätter dock att variansen för populationen (och därmed variansen för medelvärdesfördelningen) är helt känd). Vid små stickprov är skattningen av variansen osäker, varför man måste ersätta 1.96 med ett annat något större tal, t. Storleken på t bestäms av stickprovets storlek, och kan hämtas från en t-tabell. Notera att t också är avhängigt konfidensintervallets procentsats.
Tabell över olika
stickprovsparametrar som beskriver variabilitet. Efter tabell 5.2 i
Underwood, Experiments in Ecology. Skattad parameter Symbol Syfte Stickprovets varians S2 Skattar populationens
varians. Beskriver variation på en
kvadrerad skala. Används för att jämföra
variation mellan olika populationer. Stickprovets
standardavvikelse S eller SD Skattar populationens
standardavvikelse. Beskriver variation mellan olika
replikat, mätningar, observationer, etc. Definieras som
hur mycket observationer i genomsnitt avviker från
medelvärdet. Kan också användas för att
jämföra variation mellan populationer, men har
inte lika trevliga matematiska egenskaper som
varians. Medelvärdets standard error
eller medelavvikelse se = s/roten ur n Beskriver den förväntade
variationen mellan olika medelvärdesskattningar;
medelvärdets precision. Definieras som
medelvärdenas standardavvikelse. Konfidensintervall CI(0.95)=xbar ±
t(0.95)*se Anger (med en viss sannolikhet,
här 95 %) inom vilket intervall de sanna
medelvärdet bör ligga. CI är liksom
se en beskrivning av precisionen i
medelvärdesskattningen.
Statistisk styrka samt alternativa metoder (5.11-5.13)
Begreppet statistisk styrka ("power") är fundamentalt inom experimentplanering. Power i ett experiment beskriver möjligheten att upptäcka en skillnad mellan behandlingar - när en sådan skillnad verkligen existerar. Det finns två typer av misstag man kan göra när man med hjälp av statistik utvärderar biologiska experiment. Detta gäller både statistik och logik (se tabell).
Feltabell
H0 Sann |
H0 Falsk |
|
Acceptera H0 |
Korrekt; =1-α |
Typ 2-fel; =β |
Förkasta H0 |
Typ 1-fel; = α |
Korrekt; =Power =1-β |
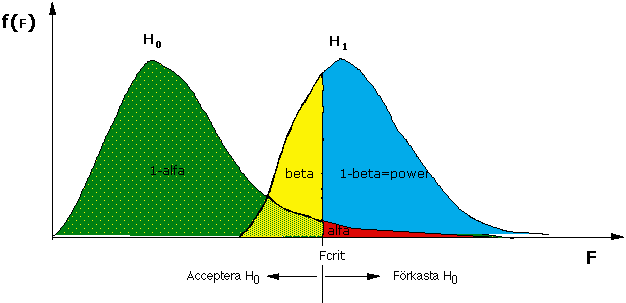
Dels finns risken att man förkastar en sann nollhypotes. Sannolikheten för att göra detta har man dock bestämt i förväg (oftast 5 %). Detta misstag kallas typ-1 fel eller α-fel (se figur). F i figuren är, liksom t, exempel på en teststatistika.

Gör man inte en analys av statistisk styrka före experimentet är sannolikheten att man skall göra ett typ-2 fel okänd, men om man gör power-analysen, så vet man hur stort experimentet behöver vara för att risken för typ-2 fel ska vara tillräckligt liten. Finns en verklig skillnad, så är den statistiska styrkan (1-β) lika med sannolikheten att förkasta en falsk nollhypotes.
I figuren kan man se att sannolikheten för typ 1 och typ 2 fel är beroende av varandra: Om vi minskar α (t.ex. α = 0.01 i stället för 0.05) så ökar Fcrit och därmed samtidigt β. Avvägningen mellan α och β bör ske med hänsyn till kostnaden av att begå det ena eller andra misstaget.
För att kunna beräkna β och power måste man känna till hur teststatistikan (t eller F) fördelar sig när H0 är falsk. När H0 är sann så fördelar sig F kring 1, men när H0 är falsk så fördelar sig F kring ett värde större än 1. Fördelningen av teststatistikan beror på:
1. Skillnaden mellan medelvärdena, effektstorlek |
A |
2. Storleken på varianserna |
σ2 |
3. Storleken på α |
α |
4. Antalet replikat |
n |
Av detta följer att jag i förväg kan beräkna hur många replikat jag behöver (= pengar och/eller tid) för att kunna, med en viss sannolikhet, detektera en viss specifierad skillnad mellan behandlingar, under förutsättning att jag har en bra skattning av varianserna.
Nyckelord
statistisk noll-hypotes, H0, test-statistika, kritiskt värde, standard error, konfidensintervall, t, statistisk styrka, power, typ-1 fel, typ-2 fel, α, β, effekt-storlek (A).
Övningsuppgifter
Du måste göra alla övningsuppgifter. Här är övningsuppgifterna till kapitel 4 och här är övningsuppgifterna till kapitel 5. Då märker du om du har förstått innehållet och om du kan använda dig av det du har lärt dig. Observera att vi förutsätter att du gör alla övningsuppgifter, även om du inte behöver redovisa alla lösningar i examinationen.