Avsnitt 4 Enfaktorsanalyser (kap 6-8)

Avsnitt 4 Övningar

1. En forskare ville testa modellen att den procentuella tillväxten hos Ascophyllum nodosum (en vanlig algart) påverkas av UV-ljus. Hon tog därför in 10 algindivider, mätte biomassan och lade dem i separata akvarier som fick stå på Tjärnölaboratoriets brygga. Efter en vecka vägde hon dem igen, lade tillbaka dem och monterade lampor som avgav UV-ljus ovanför akvarierna. Efter ytterligare en vecka vägde hon dem åter och avslutade experimentet. Tabellen nedan visar vilka vikter som observerades.

Storlek

Individ Vecka 0 Vecka 1 Vecka 2

1 31.084 32.259 32.999

2 32.809 35.524 36.063

3 30.693 31.159 31.336

4 33.691 35.812 37.174

5 34.509 36.930 38.079

6 30.771 31.886 31.921

7 30.285 32.418 32.939

8 31.802 33.151 34.784

9 33.562 36.503 37.078

10 31.510 32.466 34.343

a. Skilde sig den procentuella tillväxten hos algerna före respektive efter de utsattes för höga UV-doser?

b. Tycker du att experimentet är väl utformat för att undersöka modellen att UV-ljus påverkar tillväxten hos algen? Motivera din ståndpunkt!

2. En forskare som nyligen jobbat i en stad med anknytning till OS gjorde i ett av denna stads estuarier en studie för att testa modeller om hur sedimentets (sandens) sammansättning påverkar djuren som lever där. Som en liten del i undersökningen mätte han halten av organiskt material i sedimentet i med fyra prover i vardera av två vikar. En kollega säger åt honom att använda t-test, men eftersom personen i fråga är ett "ANOVA-freak" kan han inte göra t-test. Hjälp honom testa om halten av organiskt material skiljer sig mellan vikarna! Glöm inte kolla om antagandet om varianshomogenitet tillåter test med t-test. Data finns i tabellen nedan.

Medel SD

Vik 1 0.853 0.125

Vik 2 1.482 0.225

3. Vilka antagande måste vara uppfyllda för att man skall kunna använda variansanalys?

4. Förklara vad som menas med att ett experiment har en balanserad design.

5. Vilken betydelse har det om ett experiment har en balanserad eller obalanserad design.

6. Vad menas med begreppet psuedoreplikering.

7. Förklara med ett exempel vad som menas med att behandlingar i ett experiment är "icke-oberoende" av varandra.

8. Vilka konsekvenser får det för tolkningen av ditt exempel om behandlingarna är icke-oberoende.

9. Du avser att testa om tre stickprovsmedelvärden är statistiskt skilda från varandra. Varianserna i de tre stickproven (n=7) är: 9, 68 och 12. Uppfyller varianserna kraven för variansanalys? Om inte: vad kan du göra då?

10. En marinbiolog undersökte antalet hjärtmussellarver per kvadratcentimeter sediment på fyra lokaler i Gullmarsfjorden juni 1998. På varje lokal togs fem sedimentproppar med ytan 1 kvadratcentimeter. Var det någon skillnad mellan lokaler? Fundera på om lokaler är nivåer i en "fixed" eller" random" faktor. Gör dina uträkningar i MS Excel på två sätt: dels med formler (som du antingen skriver själv eller hämtar via formelhanteraren på verktygsraden) och dels med hjälp av funktioner i "Data analys".

A B C D

10 20 15 5

12 21 9 3

9 19 13 6

11 23 14 6

10 18 8 4

11. Nedanstående dataset beskriver antal dagar som individuella knubbsälshanar vistades på land under 1999 i förhållande till ålder (A=adulta; S= subadulta; J=juvenila). Var det någon skillnad mellan livsstadier?

Tid på land

A S J

47 24 10

49 36 13

55 50 15

57 50 17

57 52 20

59 53 21

60 55 21

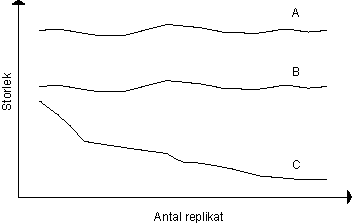
12. Identifiera i den schematiska figuren vilka linjer (A, B och C) som motsvarar hur värdena för de skattade standardavvikelserna (s), varianserna (s2) och standardfelet ("standard error"; SE) förändras när antalet replikat ökar.

13. I kapitel 7 i boken används många uttryck och symboler för att illustrera grunderna i variansanalys. Uttrycken och symbolerna återkommer på flera ställen i texten där de används i olika sammanhang. Dessutom finns det i flera fall synonymer samt uttryck på svenska som inte alltid är ordagranna översättningar. I sammanfattningen på kursen webbplats och i Excel dyker det upp ännu fler beteckningar.

I denna uppgift kan du öva viktiga begrepp och symboler. I tabeller och figurer har vi bytt ut vissa beteckningar mot inringade siffror. I detta PDF dokument finns listat en del begrepp, symboler och formler. Din uppgift blir att föra ihop det som står för samma sak enlig detta exempel:

nollhypotesen = H0 = 29 = 30.

14. I en planerad marin recipientkontroll är man intresserad av att undersöka om biomassan av fintrådiga alger skiljer sig mellan ett referensområde , en recipient från ett reningsverk med endast fosforrening och en recipient från ett reningsverk med både fosfor och kväverening. Målet har ställts till att med 90% säkerhet kunna upptäcka en eventuell ökning i någon (eller båda) recipienterna med 10 g torrvikt m^-2 jämfört med referensområdet. För att kunna dimensionera montoringprogrammet gjordes en pilotstudie där nedanstående data erhölls. Ge förslag på hur många replikat som kommer att behövas i recipientkontrollen.

Referensområde: 10, 20, 15

Reningsverk med fosfor: 35, 18, 28

Reningsverk med fosfor och kväve: 19, 8, 25

15. Finns det några problem med ovanstående program?

Lycka till!