
Enfaktorsanalyser (kap 6-8)

|
|
Enfaktorsanalyser (kap 6-8) |
 |
Avsnitt 4 - Svar på
övningar
1. En forskare ville testa modellen att den procentuella tillväxten hos Ascophyllum nodosum (en vanlig algart) påverkas av UV-ljus. Hon tog därför in 10 algindivider, mätte biomassan och lade dem i separata akvarier som fick stå på Tjärnölaboratoriets brygga. Efter en vecka vägde hon dem igen, lade tillbaka dem och monterade lampor som avgav UV-ljus ovanför akvarierna. Efter ytterliagare en vecka vägde hon dem åter och avslutade experimentet. Tabellen nedan visar vilka vikter som observerades.
Storlek
Individ Vecka 0 Vecka 1 Vecka 2
1 31.084 32.259 32.999
2 32.809 35.524 36.063
3 30.693 31.159 31.336
4 33.691 35.812 37.174
5 34.509 36.930 38.079
6 30.771 31.886 31.921
7 30.285 32.418 32.939
8 31.802 33.151 34.784
9 33.562 36.503 37.078
10 31.510 32.466 34.343
a. Skilde sig den procentuella tillväxten hos algerna före respektive efter de utsattes för höga UV-doser?
b. Tycker du att experimentet är väl utformat för att undersöka modellen att UV-ljus påverkar tillväxten hos algen? Motivera din ståndpunkt!
Svar: a. Den procentuella tillväxten var 5.4 och 2.5% före respektive efter algerna utsattes för UV-ljus. Det observerade t-värdet var 2.80 och sannolikheten för detta är 0.021 om H0 är sann. Vi förkastar alltså H0 om ingen skillnad! [Tips: tillväxten skall mätas i procentuella termer.] Se excelfil
b. Experimentet är OK om man vill uttala sig om skillnader i tillväxten skiljer sig mellan de två mätperioderna. Detta är inte samma som att eventuella skillnader är orsakade av UV. Andra faktorer såsom, temperatur, soldjus, regn, syrehalt i vattnet, hantering av algerna och ett oändliugt antal andra faktorer kan ha orsakat skillnaderna. För att dra slutsatser om UV-ljustets betydelse behövs kontroller som inte utsätts för ökat UV-ljus!
2. En anonym person som nyligen jobbat i en stad med anknytning till OS gjorde i ett av denna stads estuarier en studie för att testa modeller om hur sedimentets (sandens) sammansättning påverkar djuren som lever där. Som en liten del i undersökningen mätte han halten av organiskt material i sedimentet i med fyra prover i vardera av två vikar. En kollega säger åt honom att använda t-test, men eftersom personen i fråga är ett "ANOVA-freak" kan han inte göra t-test. Hjälp honom testa om halten av organiskt material skiljer sig mellan vikarna! Glöm inte kolla om antagandet om varianshomogenitet tillåter test med t-test. Data finns i tabellen nedan.
Medel SD
Vik 1 0.853 0.125
Vik 2 1.482 0.225
Svar: Använd F-test för att testa varianshomgenitet (stycke 6.4.2). Detta kan göras i excel med funktionen "=FFÖRD(F;3;3)". I detta fall blir F = 3.23 vilket resulterar i p = 0.18. Vi kan alltså använda oss av t-test. Det observerade värdet av t kan beräknas till 4.89 med hjälp av formeln på sidan 111. Sannolikheten för detta värde är mindre än 0.01 om H0 är sann. Vi förkastar alltså H0!
3. Vilka antagande måste vara uppfyllda för att man skall kunna använda variansanalys?
Svar: Homogena varianser, normalfördelade data, oberoende data (samt summations-antagandet)
4. Förklara vad som menas med att ett experiment har en balanserad design.
Svar: Antalet replikat är lika stort i alla behandlingar.
5. Vilken betydelse har det om ett experiment har en balanserad eller obalanserad design.
Svar: Om designen är obalanserad så kommer precisionen i skattningen av medelvärdet att vara sämre i de behandlingar som har färre replikat. Detta medför att dessa behandlingars medelvärden kommer att vara svårare att skilja statistiskt från de övriga medelvärdena.
6. Vad menas med begreppet psuedoreplikering.
Svar: Psuedoreplikering innebär att det finns ett beroende mellan replikat inom behandling. Om du har tre akvarier med fem fiskar i varje akvarium och sedan utsätter varje akvarium för en behandling, så är fiskarna psuedoreplikat. Dvs n=1.
7. Förklara med ett exempel vad som menas med att behandlingar i ett experiment är "icke-oberoende" av varandra. och 8. Vilka konsekvenser får det för tolkningen av ditt exempel om behandlingarna är icke-oberoende.
Svar: Se exempel 11 nedan med sälar. Om du konsekvens mäter adulter och juveniler samtidigt på samma kobbe så löper du risken att antingen underskatta skillnaden i tid (om adulterna är mödrar till juvenilerna) eller överskatta skillnaden (om adulterna är hannar).
9. Du avser att testa om tre stickprovsmedelvärden är statistiskt skilda från varandra. Varianserna i de tre stickproven (n=7) är: 9, 68 och 12. Uppfyller varianserna kraven för variansanalys?Om inte: vad kan du göra då?
Svar:C=största variansen delat med summan av variansena blir 0.764. Det kritiska värdet, Ccrit, är (df. k=3 och v=6): 0.6771. Eftersom C>Ccrit så är det mindre än fem % sannolikhet att den största variansen är så pass mycket större av rena slumpskäl. Slusatsen är att antagandet för variansanalys inte är uppfyllt eftersom varianserna är heterogena. Man kan försöka att transformera originaldata; dessa har vi dock inte tillgång till här.
10. En marinbiolog undersökte antalet hjärtmussellarver per kvadratcentimeter sediment på fyra lokaler i Gullmarsfjorden juni 1998. På varje lokal togs fem sedimentproppar med ytan 1 kvadratcentimeter. Var det någon skillnad mellan lokaler? Fundera på om lokaler är nivåer i en "fixed" eller" random" faktor. Gör dina uträkningar i MS Excel på två sätt: dels med formler (som du antingen skriver själv eller hämtar via formelhanteraren på verktygsraden) och dels med hjälp av funktioner i "Data analys".
A B C D
10 20 15 5
12 21 9 3
9 19 13 6
11 23 14 6
10 18 8 4
Svar: Ja det var skillnad. Om du endast är intresserad av dessa 4 lokaler, så var samtliga parvisa jämförelser signifikanta utom mellan lokal A och C. Se även Excelblad Svarstal4.xls
11. Nedanstående dataset beskriver antal dagar som individuella knubbsälshanar vistades på land under 1999 i förhållande till ålder (A=adulta; S= subadulta; J=juvenila). Var det någon skillnad mellan livsstadier?
Tid på land
A S J
47 24 10
49 36 13
55 50 15
57 50 17
57 52 20
59 53 21
60 55 21
Svar: Adulter och subadulter tillbringar mer tid på land än juveniler. Eftersom varianserna var heterogena transformerades data med ln(x). Excelblad Svarstal4.xls
12. Identifiera i den schematiska figuren vilka linjer (A, B och C) som motsvarar hur värdena för de skattade standardavvikelserna (s), varianserna (s2) och standardfelet ("standard error"; SE) förändras när antalet replikat ökar.
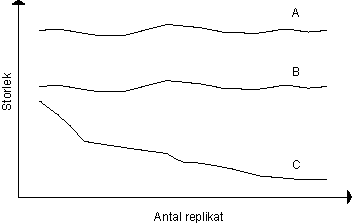
Svar: A. Variansen
B. Standardavvikelsen
C. Standardfelet = Standard error
Notera att variansen och standardavvikelsen INTE minskar när stickprovstorleken ökar (däremot blir SKATTNINGEN av dessa parametrar bättre när n ökar). Standard error däremot, som ju är ett mått på hur upprepade stickprovsmedelvärden varierar, minskar givetvis när n ökar (även skattningen av s.e. blir bättre när n ökar).
13.
antalet mätvärden i varje population = Antalet replikat i varje population = Count = n = 5 = 16 = 19 = 23 = 26
antalet populationer i analysen = a = 2 = 7 = 18 = 22 = 24
beteckning på en av populationerna (vilken som helst) i analysen = Beteckning på en av behandlingarna (vilken som helst) = i = 1
beteckning på ett av replikaten (vilket som helst) inom en population = j = 3
det uppskattade medelvärdet för en av populationerna = xbari = 6 = 8 = 9 = 17
förhållandet mellan två uppskattningar av en varians när nollhypotesen är sann = teststatistika för variansanalys = F&endash;kvot (som alltid är MSamong/MSwithin för envägs variansanalys)
Mean square = medelkvadratsumma = MS
medelkvadratsumman inom prover = MSinom = MSwithin = MSerror = MSresidual = 31
medelkvadratsumman mellan prover = MSmellan = MSamong = MSbetween = MStreatment = 32
måttet på hur långt varje Xij är från sin populations medelvärde = eij = 11 = 13
nollhypotesen = H0 = 29 = 30
Sum of squares = kvadratsumman = SS
The linear difference between the mean of population i and the mean of all populations, if the null hypothesis is not true = Ai = 12 = 14 = 15 = 21
Total sum of squares = den totala kvadratsumman
variabels mätvärde på något av replikaten som hör till någon av populationerna = Xij = 4 = 10 = 25 28
variabelns skattade medelvärde för hela populationen = Xbar = 20
Variance of all of the populations = Variance of each of the populations = s2e (när villkoren för variansanalys är uppfyllda) = 27
14. Det behövs 13 replikat för att kunna upptäcka en skillnad på 10 g med 90 % power.
Se excelbladet svar5.xls
15. Undersökningen är egentligen psuedoreplikerad eftersom det endast är ett område av varje typ. Fler reningsverk kan ibland vara svårt att åstadkomma, men ytterliggare referensområden bör man ha.
Senast ändrad: 20 februari
2001
Av:
carl.andre@tmbl.gu.se